What Must You Know to Construct a Particular Binomial Probability? Course Hero

Discrete Random Variables

Binomial Distribution

There are three characteristics of a binomial experiment.

1. There are a fixed number of trials. Think of trials as repetitions of an experiment. The letter n denotes the number of trials.
2. At that place are only two possible outcomes, called "success" and "failure," for each trial. The letter p denotes the probability of a success on one trial, and q denotes the probability of a failure on ane trial. p + q = 1.
3. The due north trials are independent and are repeated using identical atmospheric condition. Because the north trials are independent, the upshot of one trial does not aid in predicting the outcome of another trial. Another way of saying this is that for each individual trial, the probability, p, of a success and probability, q, of a failure remain the same. For example, randomly guessing at a true-false statistics question has simply two outcomes. If a success is guessing correctly, so a failure is guessing incorrectly. Suppose Joe always guesses correctly on whatever statistics true-false question with probability p = 0.6. And so, q = 0.4. This means that for every true-false statistics question Joe answers, his probability of success (p = 0.6) and his probability of failure (q = 0.4) remain the same.

The outcomes of a binomial experiment fit a binomial probability distribution. The random variable X = the number of successes obtained in the n contained trials.

The mean, μ, and variance, σ ⁱⁱ, for the binomial probability distribution are μ = np and σ ² = npq. The standard deviation, σ, is then σ = .

Any experiment that has characteristics two and three and where n = one is chosen a Bernoulli Trial (named after Jacob Bernoulli who, in the late 1600s, studied them extensively). A binomial experiment takes identify when the number of successes is counted in one or more Bernoulli Trials.

At ABC College, the withdrawal charge per unit from an elementary physics course is xxx% for any given term. This implies that, for any given term, 70% of the students stay in the grade for the entire term. A "success" could be defined equally an individual who withdrew. The random variable X = the number of students who withdraw from the randomly selected elementary physics grade.

Effort It

The state wellness lath is concerned nearly the amount of fruit available in schoolhouse lunches. Forty-eight percent of schools in the state offer fruit in their lunches every solar day. This implies that 52% exercise non. What would a "success" exist in this case?

Suppose you play a game that you tin only either win or lose. The probability that you lot win any game is 55%, and the probability that y'all lose is 45%. Each game you lot play is independent. If you play the game xx times, write the office that describes the probability that yous win xv of the 20 times. Here, if you define X equally the number of wins, then X takes on the values 0, 1, two, 3, …, 20. The probability of a success is p = 0.55. The probability of a failure is q = 0.45. The number of trials is n = 20. The probability question tin can be stated mathematically equally P(x = fifteen).

Try Information technology

A trainer is teaching a dolphin to exercise tricks. The probability that the dolphin successfully performs the fob is 35%, and the probability that the dolphin does not successfully perform the trick is 65%. Out of xx attempts, you want to find the probability that the dolphin succeeds 12 times. Country the probability question mathematically.

A off-white coin is flipped 15 times. Each flip is independent. What is the probability of getting more than ten heads? Allow X = the number of heads in 15 flips of the fair money. X takes on the values 0, i, 2, iii, …, 15. Since the coin is fair, p = 0.5 and q = 0.5. The number of trials is north = 15. State the probability question mathematically.

Try It

A fair, six-sided die is rolled ten times. Each coil is independent. You lot want to discover the probability of rolling a one more three times. State the probability question mathematically.

Approximately seventy% of statistics students do their homework in time for it to be nerveless and graded. Each educatee does homework independently. In a statistics class of 50 students, what is the probability that at least forty will do their homework on time? Students are selected randomly.

a. This is a binomial trouble because at that place is only a success or a __________, there are a fixed number of trials, and the probability of a success is 0.70 for each trial.

b. If we are interested in the number of students who do their homework on fourth dimension, and then how do nosotros ascertain X?

b. X = the number of statistics students who do their homework on fourth dimension

c. What values does x accept on?

d. What is a "failure," in words?

d. Failure is defined as a student who does not complete his or her homework on fourth dimension.

The probability of a success is p = 0.70. The number of trials is n = 50.

east. If p + q = 1, then what is q?

f. The words "at least" interpret as what kind of inequality for the probability question P(x ____ 40).

f. greater than or equal to (≥)
The probability question is P(x ≥ 40).

Endeavor It

Sixty-five percent of people laissez passer the country driver's exam on the first try. A grouping of l individuals who have taken the driver's exam is randomly selected. Give ii reasons why this is a binomial problem.

Notation for the Binomial: B = Binomial Probability Distribution Function

Ten ~ B(north, p)

Read this as "X is a random variable with a binomial distribution." The parameters are n and p; northward = number of trials, p = probability of a success on each trial.

It has been stated that about 41% of developed workers have a high school diploma just do not pursue any further didactics. If 20 adult workers are randomly selected, discover the probability that at virtually 12 of them accept a loftier school diploma but do not pursue any further teaching. How many developed workers exercise you expect to have a high school diploma just do not pursue whatsoever further education?

Let X = the number of workers who have a high school diploma simply do not pursue whatsoever further didactics.

X takes on the values 0, 1, 2, …, 20 where n = 20, p = 0.41, and q = 1 – 0.41 = 0.59. 10 ~ B(20, 0.41)

Find P(x ≤ 12). P(x ≤ 12) = 0.9738. (calculator or computer)

Get into ii^nd DISTR. The syntax for the instructions are as follows:

To calculate (10 = value): binompdf(n, p, number) if "number" is left out, the result is the binomial probability table.
To calculate P(x ≤ value): binomcdf(n, p, number) if "number" is left out, the result is the cumulative binomial probability table.
For this trouble: After you are in two^nd DISTR, pointer down to binomcdf. Press ENTER. Enter twenty,0.41,12). The result is P(x ≤ 12) = 0.9738.

Note

If you want to notice P(x = 12), use the pdf (binompdf). If you want to discover P(ten > 12), employ ane – binomcdf(20,0.41,12).

The probability that at most 12 workers take a loftier schoolhouse diploma but exercise not pursue whatever further education is 0.9738.

The graph of X ~ B(20, 0.41) is as follows:

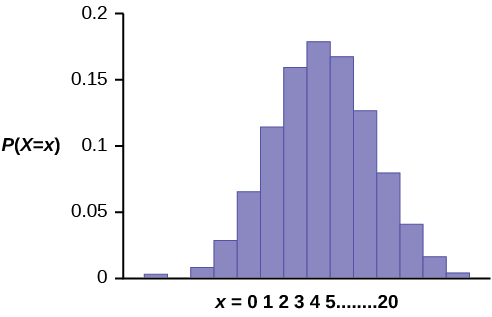
The y-axis contains the probability of 10, where Ten = the number of workers who take only a loftier school diploma.

The number of developed workers that you expect to accept a high schoolhouse diploma but not pursue whatsoever further education is the mean, μ = np = (20)(0.41) = 8.2.

The formula for the variance is σ² = npq. The standard deviation is σ = .
σ = = two.20.

Try It

About 32% of students participate in a community volunteer plan outside of schoolhouse. If 30 students are selected at random, discover the probability that at most 14 of them participate in a community volunteer program exterior of school. Use the TI-83+ or TI-84 figurer to find the respond.

In the 2013 Jerry's Artarama art supplies catalog, there are 560 pages. Eight of the pages feature signature artists. Suppose we randomly sample 100 pages. Let X = the number of pages that characteristic signature artists.

1. What values does ten accept on?
2. What is the probability distribution? Notice the post-obit probabilities:
   1. the probability that two pages feature signature artists
   2. the probability that at most six pages characteristic signature artists
   3. the probability that more than iii pages feature signature artists.
3. Using the formulas, calculate the (i) hateful and (ii) standard deviation.

Endeavor Information technology

According to a Gallup poll, 60% of American adults adopt saving over spending. Let 10 = the number of American adults out of a random sample of 50 who prefer saving to spending.

1. What is the probability distribution for X?
2. Use your calculator to notice the following probabilities:
   1. the probability that 25 adults in the sample prefer saving over spending
   2. the probability that at most xx adults prefer saving
   3. the probability that more 30 adults adopt saving
3. Using the formulas, calculate the (i) mean and (ii) standard deviation of X.

The lifetime risk of developing pancreatic cancer is well-nigh one in 78 (1.28%). Suppose we randomly sample 200 people. Allow X = the number of people who volition develop pancreatic cancer.

1. What is the probability distribution for X?
2. Using the formulas, calculate the (i) hateful and (ii) standard deviation of X.
3. Use your calculator to discover the probability that at well-nigh eight people develop pancreatic cancer
4. Is it more likely that five or vi people will develop pancreatic cancer? Justify your answer numerically.

Endeavor Information technology

During the 2013 regular NBA season, DeAndre Hashemite kingdom of jordan of the Los Angeles Clippers had the highest field goal completion rate in the league. DeAndre scored with 61.3% of his shots. Suppose yous choose a random sample of lxxx shots fabricated by DeAndre during the 2013 season. Allow 10 = the number of shots that scored points.

1. What is the probability distribution for Ten?
2. Using the formulas, summate the (i) mean and (2) standard deviation of Ten.
3. Use your calculator to detect the probability that DeAndre scored with lx of these shots.
4. Observe the probability that DeAndre scored with more 50 of these shots.

The following case illustrates a problem that is non binomial. It violates the condition of independence. ABC College has a student advisory commission fabricated up of x staff members and half-dozen students. The committee wishes to choose a chairperson and a recorder. What is the probability that the chairperson and recorder are both students? The names of all committee members are put into a box, and two names are drawn without replacement. The kickoff name drawn determines the chairperson and the second name the recorder. There are ii trials. However, the trials are not independent considering the outcome of the first trial affects the consequence of the second trial. The probability of a student on the first draw is . The probability of a educatee on the second draw is , when the first draw selects a educatee. The probability is , when the first draw selects a staff member. The probability of drawing a student's name changes for each of the trials and, therefore, violates the status of independence.

Try It

A lacrosse team is selecting a captain. The names of all the seniors are put into a hat, and the kickoff three that are drawn volition be the captains. The names are not replaced once they are drawn (ane person cannot be two captains). You want to meet if the captains all play the same position. State whether this is binomial or non and state why.

Chapter Review

A statistical experiment tin can be classified every bit a binomial experiment if the following atmospheric condition are met:

1. There are a stock-still number of trials, due north.
2. There are only two possible outcomes, chosen "success" and, "failure" for each trial. The letter p denotes the probability of a success on one trial and q denotes the probability of a failure on one trial.
3. The due north trials are independent and are repeated using identical atmospheric condition.

The outcomes of a binomial experiment fit a binomial probability distribution. The random variable 10 = the number of successes obtained in the northward contained trials. The mean of Ten can be calculated using the formula μ = np, and the standard deviation is given by the formula σ = .

Formula Review

X ~ B(n, p) means that the discrete random variable X has a binomial probability distribution with n trials and probability of success p.

X = the number of successes in north contained trials

northward = the number of independent trials

Ten takes on the values x = 0, 1, 2, three, …, north

p = the probability of a success for any trial

q = the probability of a failure for whatever trial

p + q = 1

q = i – p

The mean of Ten is μ = np. The standard deviation of 10 is σ = .

Apply the post-obit information to answer the adjacent 8 exercises: The College Didactics Enquiry Plant at UCLA nerveless data from 203,967 incoming first-time, full-time freshmen from 270 4-year colleges and universities in the U.South. 71.three% of those students replied that, aye, they believe that aforementioned-sex couples should take the correct to legal marital status. Suppose that you randomly choice viii first-fourth dimension, total-time freshmen from the survey. You lot are interested in the number that believes that aforementioned sex-couples should have the correct to legal marital status.

In words, define the random variable X.

X = the number that reply "yes"

X ~ _____(_____,_____)

<!– <solution id="id7617599″> B(8,0.713) –>

What values does the random variable X take on?

0, 1, ii, iii, 4, five, half dozen, vii, viii

Construct the probability distribution function (PDF).

10	P(10)

<!– <solution id="fs-idm163794480″>

–>

On boilerplate (μ), how many would you look to answer yes?

5.seven

What is the standard departure (σ)?

<!– <solution id="id8562245″> one.2795 –>

What is the probability that at most five of the freshmen reply "yes"?

0.4151

What is the probability that at least ii of the freshmen answer "yes"?

<!– <solution id="id8562331″> 0.9990 –>

HOMEWORK

According to a recent article the average number of babies built-in with significant hearing loss (deafness) is approximately two per 1,000 babies in a healthy baby nursery. The number climbs to an average of xxx per 1,000 babies in an intensive care nursery.

Suppose that one,000 babies from healthy baby nurseries were randomly surveyed. Observe the probability that exactly two babies were born deafened.

<!– <solution id="eip-idm92090528″> 0.2709 –>

Utilize the following information to answer the adjacent four exercises. Recently, a nurse commented that when a patient calls the medical advice line claiming to take the flu, the risk that he or she truly has the flu (and not just a nasty common cold) is only near 4%. Of the next 25 patients calling in claiming to have the flu, nosotros are interested in how many really have the flu.

Define the random variable and list its possible values.

10 = the number of patients calling in claiming to have the flu, who actually have the flu.

Ten = 0, 1, 2, …25

State the distribution of X.

<!– <solution id="eip-idm5232336″> B(25,0.04) –>

Notice the probability that at least 4 of the 25 patients actually have the flu.

0.0165

On average, for every 25 patients calling in, how many do yous expect to accept the flu?

<!– <solution id="eip-idm142934512″> 1 –>

People visiting video rental stores often hire more than ane DVD at a time. The probability distribution for DVD rentals per customer at Video To Go is given (Figure). There is five-video limit per customer at this store, so nobody always rents more than five DVDs.

10	P(x)
0	0.03
1	0.50
ii	0.24
three
4	0.07
5	0.04

1. Draw the random variable Ten in words.
2. Find the probability that a customer rents three DVDs.
3. Find the probability that a customer rents at least four DVDs.
4. Detect the probability that a customer rents at most two DVDs.

1. X = the number of DVDs a Video to Go customer rents
2. 0.12
3. 0.xi
4. 0.77

A schoolhouse paper reporter decides to randomly survey 12 students to encounter if they volition attend Tet (Vietnamese New year) festivities this yr. Based on by years, she knows that xviii% of students nourish Tet festivities. We are interested in the number of students who volition attend the festivities.

1. In words, define the random variable X.
2. List the values that X may take on.
3. Requite the distribution of 10. X ~ _____(_____,_____)
4. How many of the 12 students do we expect to attend the festivities?
5. Find the probability that at most iv students volition attend.
6. Find the probability that more than 2 students volition attend.

<!– <solution id="id17988422″> 10 = the number of students who will attend Tet. 0, 1, two, 3, 4, 5, 6, seven, 8, 9, 10, 11, 12 X ~ B(12,0.18) 2.xvi 0.9511 0.3702 –>

Use the following information to answer the side by side ii exercises: The probability that the San Jose Sharks will win any given game is 0.3694 based on a 13-twelvemonth win history of 382 wins out of 1,034 games played (every bit of a certain date). An upcoming monthly schedule contains 12 games.

The expected number of wins for that upcoming month is:

1. 1.67
2. 12
3. 
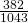
4. four.43

d. 4.43

Let X = the number of games won in that upcoming calendar month.

What is the probability that the San Jose Sharks win half dozen games in that upcoming calendar month?

1. 0.1476
2. 0.2336
3. 0.7664
4. 0.8903

<!– <solution id="id17994552″> a –>

What is the probability that the San Jose Sharks win at least five games in that upcoming month

1. 0.3694
2. 0.5266
3. 0.4734
4. 0.2305

c

A educatee takes a ten-question true-imitation quiz, but did non study and randomly guesses each answer. Find the probability that the student passes the quiz with a course of at least 70% of the questions correct.

<!– <solution id="eip-id1171731523478″> 10 = number of questions answered correctly Ten ~ B(10, 0.five) We are interested in AT Least 70% of 10 questions correct. seventy% of ten is 7. Nosotros desire to find the probability that 10 is greater than or equal to seven. The event "at least seven" is the complement of "less than or equal to six". Using your calculator'due south distribution bill of fare: i – binomcdf(10, .five, 6) gives 0.171875 The probability of getting at least 70% of the 10 questions correct when randomly guessing is approximately 0.172. –>

A student takes a 32-question multiple-selection exam, just did non study and randomly guesses each answer. Each question has three possible choices for the answer. Find the probability that the student guesses more than 75% of the questions correctly.

Six different colored dice are rolled. Of involvement is the number of dice that show a one.

1. In words, ascertain the random variable X.
2. List the values that X may take on.
3. Give the distribution of 10. X ~ _____(_____,_____)
4. On average, how many dice would you expect to show a one?
5. Find the probability that all six dice bear witness a ane.
6. Is it more probable that 3 or that four die will show a ane? Use numbers to justify your answer numerically.

<!– <solution id="id17531763″> X = the number of dice that show a one 0, i, 2, 3, iv, 5, half-dozen X ~ B ( 6, ane vi ) 1 0.00002 three dice –>

More than 96 per centum of the very largest colleges and universities (more than 15,000 total enrollments) take some online offerings. Suppose you randomly pick 13 such institutions. We are interested in the number that offer distance learning courses.

1. In words, define the random variable X.
2. List the values that X may have on.
3. Give the distribution of X. X ~ _____(_____,_____)
4. On average, how many schools would you expect to offer such courses?
5. Detect the probability that at near 10 offering such courses.
6. Is it more likely that 12 or that 13 volition offer such courses? Use numbers to justify your answer numerically and reply in a complete sentence.

1. X = the number of higher and universities that offer online offerings.
2. 0, 1, two, …, 13
3. Ten ~ B(13, 0.96)
4. 12.48
5. 0.0135
6. P(x = 12) = 0.3186 P(x = xiii) = 0.5882 More than likely to become xiii.

Suppose that about 85% of graduating students attend their graduation. A grouping of 22 graduating students is randomly chosen.

1. In words, define the random variable Ten.
2. List the values that X may take on.
3. Requite the distribution of X. 10 ~ _____(_____,_____)
4. How many are expected to nourish their graduation?
5. Discover the probability that 17 or 18 attend.
6. Based on numerical values, would yous be surprised if all 22 attended graduation? Justify your answer numerically.

<!– <solution id="fs-idm62699008″> 10 = the number of students who nourish their graduation 0, 1, 2, …, 22 X ~ B(22, 0.85) 18.7 0.3249 P(ten = 22) = 0.0280 (less than 3%) which is unusual –>

At The Fencing Center, 60% of the fencers utilise the foil as their main weapon. We randomly survey 25 fencers at The Fencing Middle. We are interested in the number of fencers who do not use the foil as their master weapon.

1. In words, define the random variable X.
2. List the values that X may take on.
3. Requite the distribution of X. Ten ~ _____(_____,_____)
4. How many are expected to not to employ the foil equally their chief weapon?
5. Find the probability that half dozen exercise not use the foil as their main weapon.
6. Based on numerical values, would you be surprised if all 25 did not utilise foil equally their primary weapon? Justify your answer numerically.

1. X = the number of fencers who do non use the foil as their main weapon
2. 0, ane, ii, 3,… 25
3. X ~ B(25,0.twoscore)
4. x
5. 0.0442
6. The probability that all 25 not utilise the foil is about zero. Therefore, it would be very surprising.

Approximately 8% of students at a local high school participate in after-school sports all four years of high school. A group of threescore seniors is randomly called. Of involvement is the number who participated in later on-school sports all 4 years of high school.

1. In words, define the random variable X.
2. List the values that Ten may take on.
3. Give the distribution of 10. X ~ _____(_____,_____)
4. How many seniors are expected to have participated in afterwards-school sports all four years of loftier school?
5. Based on numerical values, would you exist surprised if none of the seniors participated in subsequently-school sports all four years of high schoolhouse? Justify your answer numerically.
6. Based upon numerical values, is it more likely that 4 or that five of the seniors participated in afterwards-school sports all four years of high schoolhouse? Justify your answer numerically.

<!– <solution id="fs-idm58938512″> X = the number of high school students who participate in after schoolhouse sports all iv years of high schoolhouse. 0, 1, two, …, 60 X ~ B(threescore, 0.08) four.8 Yes, P(ten = 0) = 0.0067, which is a modest probability P(x = 4) = 0.1873, P(x = v) = 0.1824. More than likely to get 4. –>

The adventure of an IRS audit for a taxation return with over ?25,000 in income is about 2% per year. We are interested in the expected number of audits a person with that income has in a 20-year period. Assume each year is independent.

1. In words, define the random variable 10.
2. Listing the values that X may accept on.
3. Give the distribution of Ten. X ~ _____(_____,_____)
4. How many audits are expected in a xx-year period?
5. Observe the probability that a person is not audited at all.
6. Find the probability that a person is audited more than than twice.

1. X = the number of audits in a twenty-twelvemonth period
2. 0, one, two, …, 20
3. X ~ B(20, 0.02)
4. 0.four
5. 0.6676
6. 0.0071

It has been estimated that only about 30% of California residents have adequate earthquake supplies. Suppose you lot randomly survey 11 California residents. We are interested in the number who take adequate earthquake supplies.

1. In words, define the random variable X.
2. List the values that X may have on.
3. Give the distribution of X. X ~ _____(_____,_____)
4. What is the probability that at least viii have adequate earthquake supplies?
5. Is information technology more probable that none or that all of the residents surveyed volition have adequate earthquake supplies? Why?
6. How many residents do you expect will have acceptable convulsion supplies?

<!– <solution id="id16028424″> X = the number of California residents who do have acceptable convulsion supplies. 0, 1, ii, 3, 4, five, 6, 7, viii, 9, x, xi B(11, 0.thirty) 0.0043 P(ten = 0) = 0.0198. P(x = 11) = 0 or none 3.3 –>

There are two similar games played for Chinese New year's day and Vietnamese New Yr. In the Chinese version, fair dice with numbers 1, 2, iii, 4, 5, and 6 are used, along with a board with those numbers. In the Vietnamese version, off-white dice with pictures of a gourd, fish, rooster, crab, crayfish, and deer are used. The board has those six objects on information technology, as well. We volition play with bets being ?1. The player places a bet on a number or object. The "business firm" rolls three die. If none of the die show the number or object that was bet, the house keeps the ?1 bet. If one of the dice shows the number or object bet (and the other two do not prove it), the player gets dorsum his or her ?1 bet, plus ?one profit. If ii of the dice testify the number or object bet (and the tertiary die does not show it), the player gets dorsum his or her ?1 bet, plus ?2 profit. If all three dice show the number or object bet, the player gets back his or her ?1 bet, plus ?three turn a profit. Let 10 = number of matches and Y = profit per game.

1. In words, define the random variable X.
2. List the values that 10 may accept on.
3. Give the distribution of X. X ~ _____(_____,_____)
4. List the values that Y may take on. Then, construct i PDF table that includes both X and Y and their probabilities.
5. Calculate the average expected matches over the long run of playing this game for the player.
6. Calculate the boilerplate expected earnings over the long run of playing this game for the histrion.
7. Determine who has the advantage, the role player or the business firm.

According to The World Bank, only 9% of the population of Republic of uganda had access to electricity as of 2009. Suppose we randomly sample 150 people in Uganda. Allow X = the number of people who have access to electricity.

1. What is the probability distribution for 10?
2. Using the formulas, calculate the mean and standard difference of 10.
3. Use your computer to find the probability that 15 people in the sample have access to electricity.
4. Find the probability that at most x people in the sample have admission to electricity.
5. Find the probability that more than 25 people in the sample have admission to electricity.

<!– <solution id="fs-idm37905376″> X ~ B(150,0.09) Mean = np = 150(0.09) = 13.5 Standard Departure = npq =   150(0.09)(0.91) ≈ 3.5050 P(x = xv) = binompdf(150, 0.09, 15) = 0.0988 P(x ≤ 10) = binomcdf(150, 0.09, 10) = 0.1987 P(x > 25) = i – P(ten ≤ 25) = 1 – binomcdf(150, 0.09, 25) = one – 0.9991 = 0.0009 –>

The literacy rate for a nation measures the proportion of people age xv and over that can read and write. The literacy charge per unit in Transitional islamic state of afghanistan is 28.i%. Suppose you choose 15 people in Afghanistan at random. Permit X = the number of people who are literate.

1. Sketch a graph of the probability distribution of X.
2. Using the formulas, calculate the (i) hateful and (ii) standard divergence of X.
3. Observe the probability that more than than five people in the sample are literate. Is it is more likely that 3 people or four people are literate.

Glossary

Binomial Experiment

a statistical experiment that satisfies the following three conditions:

1. There are a fixed number of trials, n.
2. There are but two possible outcomes, called "success" and, "failure," for each trial. The alphabetic character p denotes the probability of a success on one trial, and q denotes the probability of a failure on one trial.
3. The n trials are contained and are repeated using identical conditions.

Bernoulli Trials

an experiment with the following characteristics:

1. There are only ii possible outcomes called "success" and "failure" for each trial.
2. The probability p of a success is the same for any trial (so the probability q = one − p of a failure is the same for any trial).

Binomial Probability Distribution

a detached random variable (RV) that arises from Bernoulli trials; there are a fixed number, n, of contained trials. "Independent" means that the result of any trial (for example, trial one) does non bear upon the results of the following trials, and all trials are conducted under the same weather condition. Under these circumstances the binomial RV X is defined as the number of successes in n trials. The notation is: X ~ B(n, p). The mean is μ = np and the standard deviation is σ = 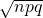. The probability of exactly 10 successes in due north trials is
P(X = x) = p ^ten q ^{north − x}.

robertseine1972.blogspot.com

Source: https://opentextbc.ca/introstatopenstax/chapter/binomial-distribution/

Share this post